Towards Neural Networks: The Modeling Problem
Thus far, we have only tackled a trivial modeling problem: using a linear model to describe the relationship between an NBA player’s height and his wingspan. In reality, we will be be interested in solving much more ambitious and diverse machine learning problems. While the paradigm of supervised learning, which we discussed in the previous section, will still be of great value to us, our choice of mathematical model is something that we will need to consider carefully. Ultimately, this discussion will lead us to work with the fabled neural network as the foundation for our mathematical models.
Let’s reflect on some typical problems that we might be interested in tackling via machine learning, and see how these can all be viewed through a unified framework.
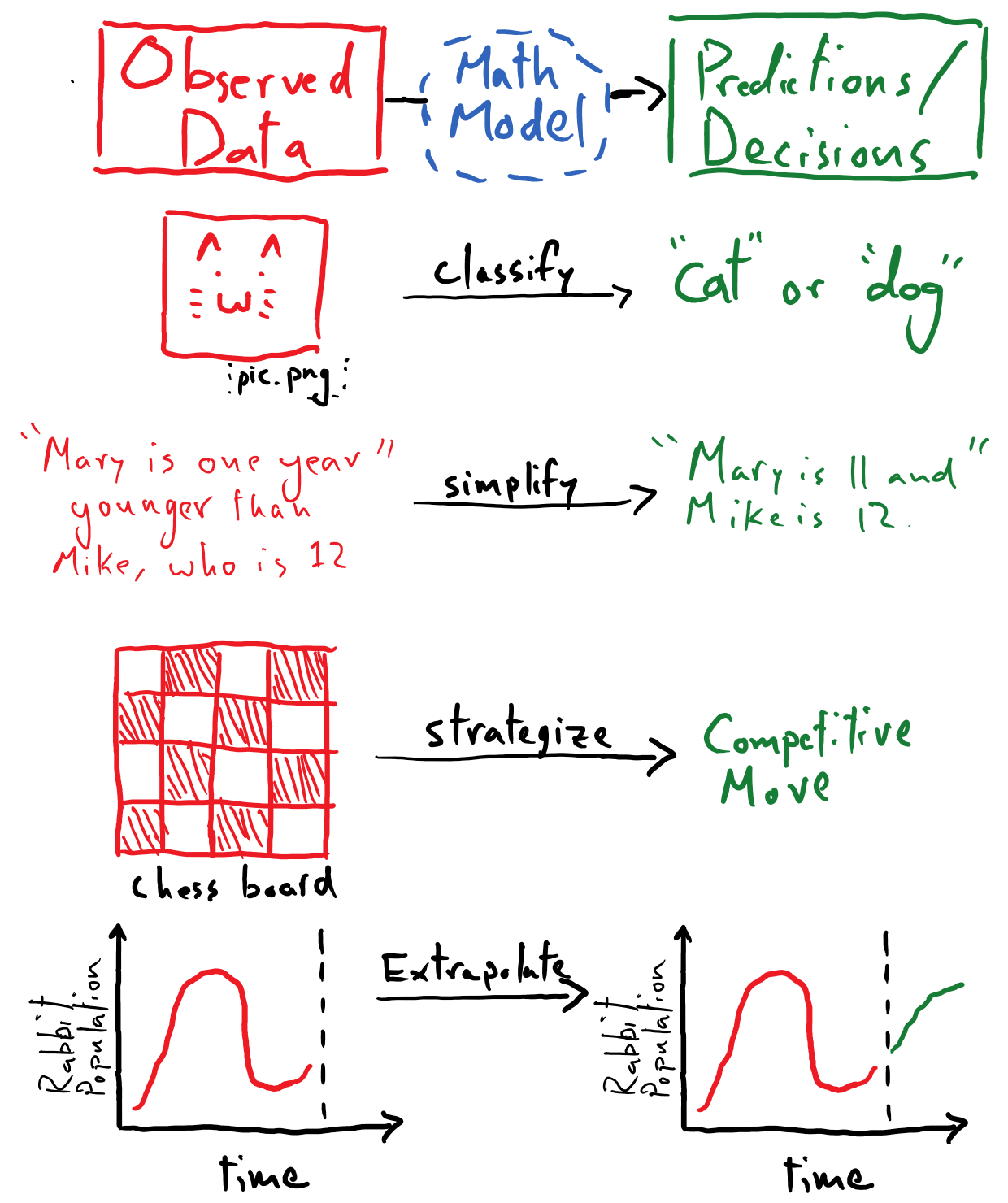
Displayed here are a diverse range of tasks that span an equally varied set of disciplines.
Image classification (computer vision)
Text comprehension (natural language processing / reasoning)
Game strategization (game artificial intelligence)
Data extrapolation / phenomenological modeling (scientific computing)
The common framework that undergirds each of these tasks is that a mathematical model will be used mediate the transformations of observations into the corresponding desired predictions or decisions. That is, we need to devise some mathematical formulation
that can process input data \(x\) (pixel-values from a picture, numerical-encodings of words in a sentence, the state of a chessboard, or a time series of data) and produce the desired output \(y^{(\mathrm{pred})}\) (classification scores for an image, the numerical-encodings for a summary sentence, a valid chess move, or extrapolated time-series values).
Furthermore, from a machine learning perspective, we want to devise these models in such a way that they are capable of improving the quality of their predictions (or decisions) based on data that we provide them with; that is, we want them to able to learn. It should be noted that a “mathematical model” need not merely be a single mathematical equation; it refers more broadly to a computer program that orchestrates a collection of mathematical equations and processes to transform the observed data into predictions or decisions.
Regardless of the fact that we hope to tackle these tasks using this common framework, the essential details of how we solve these respective problems seems to be quite different from one another. Traditionally, attempting to solve any of the above problems would require one to develop specialized knowledge in that subfield. To develop a model that can classify pictures of cats versus dogs, for instance, would lead us down the path of learning about standard computer vision methods for measuring visual features – groups of edges, “blobs”, and the like – within an image.
To provide some intuition about this, the image following depicts detected edges from a picture of a meerkat.

Here, we hand-designed an algorithmic/mathematical approach for processing the pixels of a picture and returning an array of 0’s and 1’s of the same shape as the picture. The array entry is 0 where there is no edge (which appears as a black pixel) and 1 where there is an edge (which appears as a white picture).
This is a process known as feature engineering, where we devise simplified, but rich, representations of our data that are useful for solving the problem at hand. We would then craft a model that extracts, composes, and quantifies these features in an image – it is designed to learn how these features manifest differently among pictures of cats and dogs, respectively, and thus it would assess the feature content of a given picture in order to render a final classification: cat or dog.
Now, imagine that instead of classifying the contents of a given picture, we instead want to detect human faces in a picture. We might have to devise a new set of features in order to tackle this different computer vision problem. It is expensive for us to go back to the drawing board to devise a new mathematical model, or engineer new features to be extracted from said model, each time that we tackle a new machine learning problem. This is what we refer to as the modeling problem: given a machine learning problem, how do we most efficiently design a mathematical model that is capable of solving that problem? Along these lines, are there efficient methods for developing mathematical models, which are effective across different application spaces? E.g. are there methods that enable us to rapidly develop successful computer vision models and language processing models?
The answer to this question appears to be “yes” – to a degree that we might have thought highly improbably until relatively recently.
The Role of Deep Learning
People have discovered simple, composable mathematical building blocks (often referred to as “neurons” and “layers of neurons”) that can be stacked together to create a highly “sculptable” model \(F\) (referred to as a “deep neural network”). Whereas in the previous example we were responsible for specifically choosing to use a linear model for our problem, we can instead use a neural network model, whose form is shaped chiefly by the data that we use to train it. Prior to being trained, the neural network is formless like a block of clay, and the training process can be thought as the data sculpting the model so that it captures the important patterns and relationships shared by our observed data and the desired predictions/decisions that we want our model to make. In this way, the trained neural network can reliably map new observations to useful predictions and decisions, based on the patterns that were “sculpted” into it. We will not need to hand-craft particular features for the neural network to leverage. Instead, it will organically discover useful features to extract from the data during the training progress.
Thus the booming discovery of deep learning is that deep neural networks help us solve the modelling problem, and that simple gradient-based optimization techniques are surprisingly effective for training deep networks. It is difficult to overstate how surprising this is.
In the next section we will be introduced to these foundational mathematical building blocks, which we will use to construct our own neural networks.
Representations of Data
Before we move on, it is useful to take a moment to clarify some important practical details that can be befuddling for newcomers to the field of machine learning. While the exemplar machine learning tasks laid out above are easy enough to understand, it may be wholly unobvious to see how we can use math to process a picture or a sentence. And for that matter, in what math class do we learn about mathematical functions that return “cat” or “dog” as their outputs? I remember feeling uneasy about even asking these questions the first time that I had them, so this brief section is meant to allay such concerns and to emphasize that our familiar toolkit of mathematics – linear algebra, calculus, signal processing, etc. – is still all that is in play here. You were not sick during the class on “the mathematics of predicting cat vs dog”.
Observed Data are Just Numbers
Consider the following \(594 \times 580\) greyscale picture of a cat.
![]()
This picture is stored on the computer as a rectangular array (with shape-\((594, 580)\)) of numbers. Each number tells the computer how bright it should make the corresponding pixel on the screen in order to render the image accurately; the larger the number, the brighter the pixel. In the case of a colored image, each pixel consists of three numbers instead of one, and they tell each pixel how much red, green, and blue color should be present in the pixel, respectively.
Thus doing mathematical analysis and manipulations on an image might be simpler than we would have assumed, were we to think of the picture as some impenetrable “image-format file” on our computer. When handed a png, we can easily load that image as a NumPy array and proceed from there with our analysis. While we might not yet know precisely what our mathematical approach will be to gleaning useful information from the image, we certainly are no longer in unfamiliar territory – we can definitely do “mathy” stuff to an array of numbers.
Working with text doesn’t give us quite as clean of a story as does imagery — there is no text equivalent to a pixel. Rather, a major challenge in the field of natural language processing is establishing a cogent numerical representation for text. We will discuss this matter in some considerable depth in the course’s language module. But until then, rest assured that we will quickly find ourselves in familiar mathematical territory when working with text as well: there will always be a method by which we map either characters or words to arrays of numbers. And as stated above, we can definitely do “mathy” stuff to an array of numbers.
The takeaway here is: no matter how exotic a machine learning problem may appear to be, we will always find a way to map our observations to numbers that we can do math on. This true for jpegs, videos, pdfs, “tweets”, audio recordings, etc.
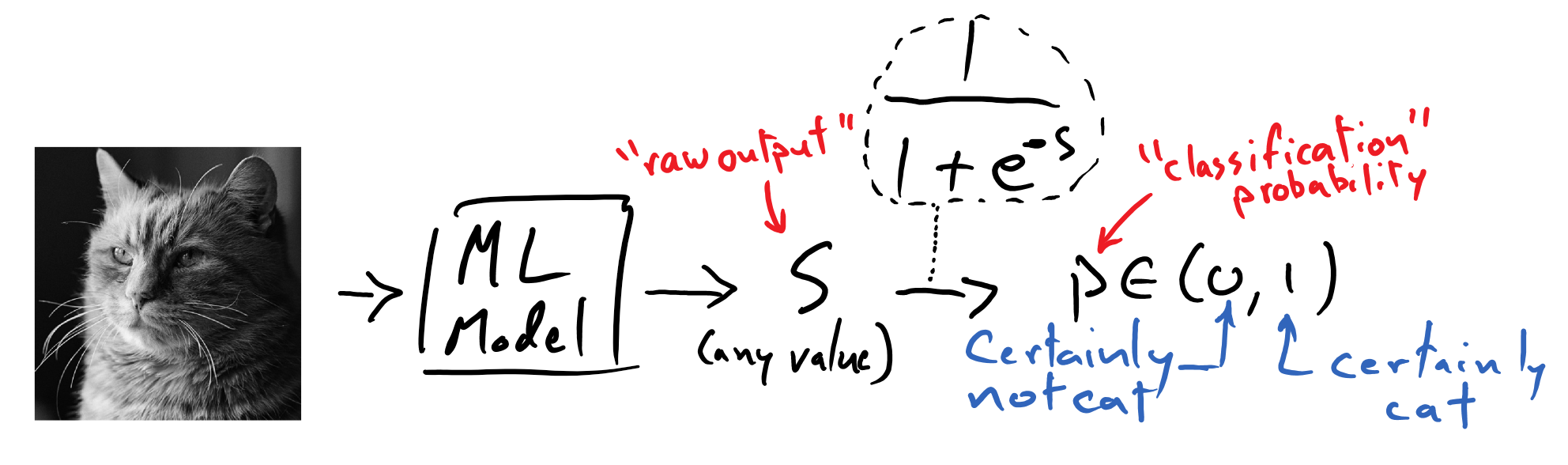
Model Predictions are Just Numbers
Finally, let’s see how we might contrive our mathematical model to produce a number that could be interpretable as a “label” of the picture’s contents.