mygrad.absolute

class mygrad.absolute(x: ArrayLike, out: Tensor | ndarray | None = None, *, where: Mask = True, dtype: DTypeLikeReals = None, constant: bool | None = None, nan_to_num: bool = True)

The absolute value, computed elementwise.

This docstring was adapted from that of numpy.absolute [1]

Parameters:

xArrayLike

Input array.

outOptional[Union[Tensor, ndarray]]

A location into which the result is stored. If provided, it must have a shape that the inputs broadcast to. If not provided or None, a freshly-allocated tensor is returned.

constantOptional[bool]

If True, this tensor is treated as a constant, and thus does not facilitate back propagation (i.e. constant.grad will always return None).

Defaults to False for float-type data. Defaults to True for integer-type data.

Integer-type tensors must be constant.

nan_to_numbool, optional (default=True)

If True then gradients that would store nans due to the presence of zeros in x will instead store zeros in those places.

whereMask

This condition is broadcast over the input. At locations where the condition is True, the out tensor will be set to the ufunc result. Elsewhere, the out tensor will retain its original value. Note that if an uninitialized out tensor is created via the default out=None, locations within it where the condition is False will remain uninitialized.

dtypeOptional[DTypeLikeReals]

The dtype of the resulting tensor.

Returns:

absoluteTensor

An ndarray containing the absolute value of each element in x.

References

[1]

Retrieved from https://numpy.org/doc/stable/reference/generated/numpy.absolute.html

Examples

>>> import mygrad as mg
>>> x = mg.array([-1.2, 1.2])
>>> mg.absolute([-1.2, 1.2])
Tensor([ 1.2,  1.2])

The absolute-value function is not differentiable at x=0.0. By default the derivative at this point is treated as 0.

>>> x = mg.tensor([-2.0, 0.0, 2.0])
>>> mg.absolute(x).backward()
>>> x.grad
np.array([-1., 0., 1.])

However a more rigorous behavior can be enabled such that the undefined derivative will be returned as nan.

>>> x = mg.tensor([-2.0, 0.0, 2.0])
>>> mg.absolute(x, nan_to_num=False).backward()
>>> x.grad
np.array([-1., nan, 1.])

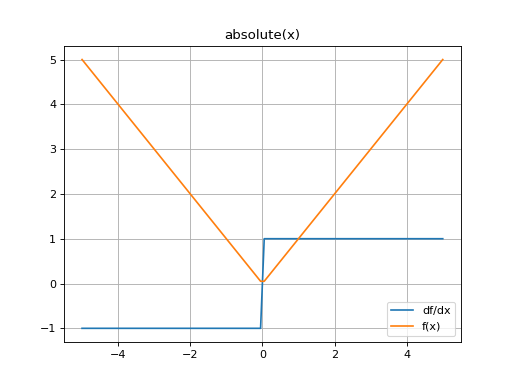
Plot the function and its derivate over [-10, 10]:

(Source code, png, hires.png, pdf)

Attributes:

identity

signature

Methods

accumulate([axis, dtype, out, constant])	Not implemented
at(indices[, b, constant])	Not implemented
outer(b, *[, dtype, out])	Not Implemented
reduce([axis, dtype, out, keepdims, ...])	Not Implemented
reduceat(indices[, axis, dtype, out])	Not Implemented
resolve_dtypes(dtypes, *[, signature, ...])	Find the dtypes NumPy will use for the operation.

__init__(*args, **kwargs)

Methods

__init__(*args, **kwargs)
accumulate([axis, dtype, out, constant])	Not implemented
at(indices[, b, constant])	Not implemented
outer(b, *[, dtype, out])	Not Implemented
reduce([axis, dtype, out, keepdims, ...])	Not Implemented
reduceat(indices[, axis, dtype, out])	Not Implemented
resolve_dtypes(dtypes, *[, signature, ...])	Find the dtypes NumPy will use for the operation.

Attributes

identity
nargs
nin
nout
ntypes
signature
types